Paradoks Zeno

Zeno dari Elea adalah seorang filsuf dari mazhab pemikiran Eleatik. Ia mengikuti jejak gurunya yang bernama Parmenides — sama-sama mempercayai bahwa semua gerak dan perubahan di dunia bersifat semu. Baik Zeno maupun Parmenides berpendapat bahwa alam semesta aslinya tunggal, diam, dan seragam. Hanya tampak luarnya saja yang mengesankan perbedaan atau perubahan.

Meskipun begitu di masa kini, hampir tidak ada karya asli Zeno dan Parmenides yang bertahan. Hanya satu-dua kutipan dari filsuf sepantaran mereka yang memberi petunjuk. Mengenai Zeno sendiri keadaannya agak menyedihkan: dikatakan bahwa aslinya dia mempunyai buku berisi 40 buah paradoks, akan tetapi buku itu kemudian hilang dicuri orang.

Untunglah, biarpun buku aslinya hilang, filsuf Aristoteles sempat mencatat sebagian di antaranya. Lewat catatan Aristoteles itu kita di masa kini dapat mengenal berbagai pemikiran Zeno. Salah satu yang terkandung dalam salinan tersebut adalah Empat Paradoks Zeno.

Terdapat empat buah paradoks Zeno sebagaimana dicatat oleh Aristoteles.Empat paradoks itu adalah:

1. Paradoks Dikotomi

“Sebuah benda yang bergerak tidak akan pernah mencapai tujuan. Pertama-tama dia harus menempuh perjalanan setengah jarak. Lalu setelah itu dia mesti menempuh seperempat, seperdelapan, seperenambelas, sepertigapuluhdua … Sedemikian hingga jumlah perjalanannya menjadi tak-hingga.

Oleh karena mustahil melakukan perjalanan sebanyak tak-hingga, maka benda tidak akan dapat sampai tujuan.”

 2. Paradoks Achilles dan Kura-kura

“Achilles dan Kura-kura melakukan lomba lari, meskipun begitu, kura-kura diizinkan start lebih awal.

Agar dapat menyamai kura-kura, Achilles menetapkan sasaran ke tempat kura-kura saat ini berdiri.

Akan tetapi, tiap kali Achilles bergerak maju, kura-kura juga bergerak maju. Ketika Achilles sampai di tempat kura-kura, kura-kura sudah berjalan sedikit ke depan.

Lalu Achilles mengejar posisi kura-kura yang sekarang. Akan tetapi setibanya di sana, kura-kura juga sudah maju sedikit lagi.

Lalu Achilles mengejar posisi kura-kura yang sekarang. Akan tetapi setibanya di sana, kura-kura juga sudah maju sedikit lagi. Demikian seterusnya ad infinitum.

Jadi kesimpulannya: mustahil bagi Achilles untuk bisa menyamai kura-kura dalam balapan.”

3. Paradoks Anak Panah

“Misalnya kita membagi waktu sebagai “deretan masa-kini”. Kemudian kita lepaskan anak panah. Di setiap “masa-kini” anak panah menduduki posisi tertentu di udara.

Oleh karena itu anak panah dapat dikatakan diam sepanjang waktu.”

4. Paradoks Stadion

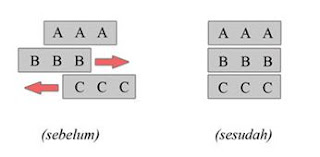
“Terdapat tiga buah barisan benda A, B, dan C di lapangan tengah stadion.

Barisan A terletak diam di tengah lapangan. Sementara B dan C masing-masing terletak di ujung kiri dan kanan A.

Kemudian B dan C bergerak saling mendekati dengan kecepatan yang sama (hendak bersejajar dengan barisan A).

Antara “Sebelum” dan “Sesudah”, titik C paling kiri melewati dua buah B, tetapi cuma satu buah A.

Berarti waktu C untuk melewati B = setengah waktu untuk melewati A. Padahal A dan B adalah unit yang identik!

Mungkinkah setengah waktu = satu waktu?”

Ada dua tema yang dominan dalam Paradoks Zeno, yakni gerak dan ketakhinggaan. Sebagaimana sudah diceritakan di awal, Zeno menganggap bahwa perubahan di dunia bersifat semu. Pendapat itu kemudian tercermin lewat empat buah paradoks di atas.

Dalam paradoks pertama (“dikotomi”), Zeno menyampaikan bahwa gerak benda antara dua titik bersifat mustahil — atau minimal, mengandung aspek filsafat yang misterius. Ada baiknya kalau kita simak lagi paradoksnya di bawah ini.

Setengah, seperempat, seperdelapan, seperenambelas…

Dalam grafik di atas digambarkan bagaimana terdapat banyak segmen perjalanan antara dua titik (0-100). Yang mengganggu Zeno di sini bukan geraknya, melainkan, bagaimana ketakhinggaan bisa begitu merepotkan. Dalam contoh di atas Zeno mengetengahkan bahwa — karena jumlah segmen yang harus ditempuh sejumlah tak-hingga — maka gerak dari satu tempat ke tempat lain adalah mustahil.

Ibaratnya begini. Apabila orang hendak berjalan menuju garis finis, maka lintasan jalannya dapat dibagi jadi bagian kecil-kecil. Kemudian supaya bisa lewat, maka bagian kecil-kecil itu harus dijalani satu per satu. Sedemikian hingga pada akhirnya orang sampai garis finis.

Akan tetapi problemnya adalah bahwa yang kecil-kecil itu jumlahnya amat banyak. Malah menurut Zeno: jumlahnya mencapai tak-hingga.

Jadi sekarang sudut pandangnya berubah. Kita tahu orang bisa menempuh jarak kecil-kecil, tetapi, bisakah orang menempuh jarak kecil-kecil itu tak berhingga kali?

Nah di sini akal mengatakan bahwa itu mustahil. Zeno sendiri akhirnya menilai bahwa gerak antara dua titik itu adalah semu. Biarpun di dunia nyata orang melakukannya dengan mudah, bukan tak mungkin bahwa itu sebenarnya hanya ilusi.

Hal yang sama juga berlaku di paradoks kedua “Achilles dan Kura-kura”. Lewat paradoks ini Zeno menyatakan bahwa “mustahil bagi orang yang telat balapan untuk dapat menyamai lawannya”.

Alasannya? Karena terdapat sejumlah kemajuan kecil-kecil yang tak mungkin dikejar. Setiap Achilles sampai di tempat kura-kura, kura-kura selalu sudah melaju sedikit lagi di depan. Pada akhirnya Achilles digambarkan Zeno sebagai “tak akan mampu melewati kura-kura”.

(keterangan: t0 melambangkan situasi pada saat pertama; t1 melambangkan situasi pada saat kedua;dan seterusnya)

Problemnya tentu saja bahwa di dunia nyata hal itu tidak berlaku, makanya disebut paradoks. Siapapun yang pernah nonton balap tahu hal ini. Pembalap yang start belakangan selalu bisa menyalip lawan di depannya. Memang kadang agak sulit melakukannya, tetapi bukan tidak mungkin.

Sebagaimana halnya dengan paradoks pertama, yang hendak disampaikan Zeno di sini adalah bagaimana konsep gerak jadi semu kalau dianalisis secara tak-hingga.

Sementara itu, lain lagi dengan paradoks ketiga tentang anak panah. Berbeda dengan sebelumnya yang ini mencoba menunjukkan bahwa “gerak” dan “diam” itu sebenarnya tak dapat dipisahkan.

Zeno melihat waktu sebagai rangkaian “masa-kini” yang berkesinambungan. Oleh karena itu sebuah anak panah yang meluncur memiliki berbagai versi “masa-kini” di perjalanannya. Ada “masa-kini” sesaat sesudah lepas dari busur; “masa-kini” setelah beberapa detik di angkasa, dan seterusnya.

Problemnya adalah bahwa di tiap “masa-kini” itu anak panah mendiami tempat yang tetap. Persis seperti kalau direkam kamera video. Di setiap frame tampak berbagai kondisi anak panah. Semua tampak diam. Akan tetapi kalau videonya diputar, barulah terkesan bahwa anak panah itu sebenarnya bergerak.

Jadi di sini ada problem: bahwa anak panah itu “diam” sekaligus “bergerak”. Pertanyaannya sekarang adalah, apakah gerak itu?

Singkat cerita, Zeno menilai bahwa paradoks anak panah menunjukkan kebenaran filsafatnya. Bahwa gerak itu aslinya semu — suatu benda terkesan bergerak cuma oleh persepsi manusia saja.

Paradoks terakhir (“Paradoks Stadion”) adalah yang paling sederhana dan kurang bermutu dibandingkan dengan yang lain.

Dalam Paradoks Stadion, Zeno mengetengahkan bahwa “dua benda yang saling mendekati butuh waktu lebih singkat untuk bisa bersejajar”. 

Sebenarnya ini adalah penerapan dari relativitas Galileo yang diajarkan di bangku SMA kita dulu. Ada yang masih ingat ceritanya? Kalau dua benda bergerak, yang satu bisa dianggap diam, sementara yang satu lagi kecepatannya dijumlahkan.

Nah demikian juga dengan kasus Paradoks Stadion di atas. Ketika B dan C sama-sama bergerak, maka jumlah waktu sebelum mereka saling bertemu juga akan mengecil, sebab kecepatannya saling menjumlahkan. Sementara A (yang tidak bergerak) tidak mendapat keuntungan tersebut. 

Sebagaimana sudah disebut beberapa kali di atas, Zeno adalah filsuf yang tidak percaya pada gerak dan perubahan. Lewat empat paradoks di atas ia ingin memastikan hakikat kenyataan sebenarnya. Sebagai seorang Eleatik Zeno berpendapat bahwa semua gerak benda itu semu; oleh karena itu, untuk membuktikan keyakinannya, ia kemudian merancang serangkaian paradoks.

ide Zeno yang menghubungkan antara kesemuan gerak dengan konsep tak-hingga. Ketika berbicara keseharian yang terbatas, ia menganalisisnya lewat serangkaian kecil-kecil yang jumlahnya mendekati tak-hingga. Pada akhirnya jalan berpikir ini menghasilkan ide baru yang segar — kalau tidak boleh dibilang absurd sama sekali.

Kalau ada di antara pembaca yang akrab dengan matematika, kemungkinan akan ngeh bahwa ide-ide Zeno punya bidang bahasannya sendiri. Keanehan Paradoks #1 dan #2, misalnya, dapat dijelaskan lewat deret konvergen. Lewat ilmu kalkulus para ahli matematika belajar bagaimana menjumlahkan irisan-irisan kecil yang jumlahnya mendekati tak-hingga. Menariknya: biarpun irisannya tak-hingga, kalau diintegralkan, ternyata jumlahnya finite. Yang semacam ini membantu menjelaskan hal-hal paradoks dalam paparan Zeno.

Bagaimana perkara keseharian yang terbatas (finite) dapat dianalisis menggunakan metode tak-hingga (infinite). Seiring dengan kemajuan ilmu matematika, konsep “ketakhinggaan dalam berhingga” (“infinity in finity”) jadi mudah dicerna. Akan tetapi ini bukan berarti semua masalah Zeno sudah selesai. Masih ada pertanyaan-pertanyaan filosofis yang perlu dijawab.

Masalahnya sendiri bukan pada bagaimana matematika menyelesaikan paradoks Zeno, melainkan, bagaimana memahami filosofi di balik jalan pikiran Zeno. Apa itu gerak? Apa sebenarnya hakikat perubahan? Seperti apakah realitas? Pertanyaan-pertanyaan di atas adalah concern filsafat yang sifatnya di luar jangkauan matematik.

Sebagaimana filsuf terkenal Bertrand Russell berkomentar secara khusus tentang Zeno,

”Zeno’s arguments, in some form, have afforded grounds for almost all theories of space and time and infinity which have been constructed from his time to ou